Example of the Calculation of the Fuzzy Tsukamoto Method

Fuzzy (Tsukamoto Method)

Example of the Tsukamoto Method

Statement

• A canned food company will produce ABC food. From the last 1 month's data, the biggest demand is up to 5000 packs/day, and the smallest demand is up to 1000 packs/day. Inventory of goods in the warehouse is up to 600 packs/day at most, and at least up to 100 packs/day. With all the limitations, until now, the company has only been able to produce a maximum of 7,000 packs of goods/day, and for the sake of machine and human resource efficiency, it is hoped that the company will produce at least 2,000 packs per day.

Rule

If the company's production process uses 4 rules as follows:

    1.    Rule 1

           IF demand DOWN and supply LOTS THEN production of goods LESS

    2.    Rule 2

           IF demand goes DOWN and supply is LITTLE THEN production of goods is LESS

    3.    Rule 3

           IF demand goes UP and supply is MUCH THEN production of goods INCREASES

    4.    Rule 4

           IF demand UP and supply SLOW THEN production of goods INCREASES

Question

• How many packages of food type ABC should be produced, if the number of requests is 3,500 packages, and the inventory in the warehouse is still 300 packages? (Use the LINEAR membership function)

Answer

• There are 3 variables used: DEMAND, SUPPLY, and PRODUCTION

          1.    DEMAND: 1000 – 5000, x = 3500

          2.    INVENTORY: 100 - 600, y = 300

          3.    PRODUCTION: 2000 – 7000, z = ?

• DEMAND, consists of 2 fuzzy sets: DOWN and UP

• The formula to use :

• The membership value for the DEMAND value = 3500

        x = 3500

µ requestDOWN[3500] = (5000 – 3500) / 4000 = 0,375

µ requestUP [3500]   = (3500 – 1000) / 4000 = 0,625

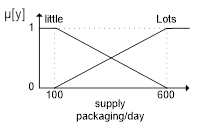
• INVENTORY, consists of 2 fuzzy sets: LITTLE and LOTS

• Formula to be used:

• Membership value for SUPPLY value = 500

            y = 300

µ suppliesaLITTLE[300] = (600 – 300) / 500 = 0,6

µ suppliesaLOST [300] = (300 – 100) / 500 = 0,4

• Demand value = 3500                  Total supply = 300

Value α- predicate and Z of each rule

Rule 1

α-predicate1 = µrequestDOWN ᴖ µsuppliesaLOST

        = min (µrequestDOWN[3500] ᴖ µsuppliesaLOST[300])

        = min (0,375 ; 0,4)

        = 0,375

From the set of goods production LESS

Z1 = (7000 – Z) / 5000 = 0,375

= 5125

Rule 2

α-predicate2 = µrequestDOWN ᴖ µsuppliesaLITTLE

        = min (µrequestDOWN[3500] ᴖ µsuppliesaLITTLE [300])

        = min (0,375 ; 0,6)

        = 0,375

From the set of goods production LESS

Z2 = (7000 – Z) / 5000 = 0,375

= 5125

Rule 3

α-predicate3 = µrequestUP ᴖ µsuppliesaLOST

        = min (µrequestUP [3500] ᴖ µsuppliesaLOST [300])

        = min (0,625 ; 0,4)

        = 0,4

From the set of ADDED goods production

Z3 = (Z – 2000) / 5000 = 0,4

= 4000

Rule 4

α-predicate4 = µrequestUP ᴖ µsuppliesaLITTLE

        = min (µrequestUP [3500] ᴖ µsuppliesaLITTLE [300])

        = min (0,625 ; 0,6)

        = 0,6

From the set of ADDED goods production

Z4 = (Z – 2000) / 5000 = 0,6

= 5000

• Calculating final Z by averaging all weighted Z's:

Results

• So, the number of ABC type foods that must be produced is 4825 packages.